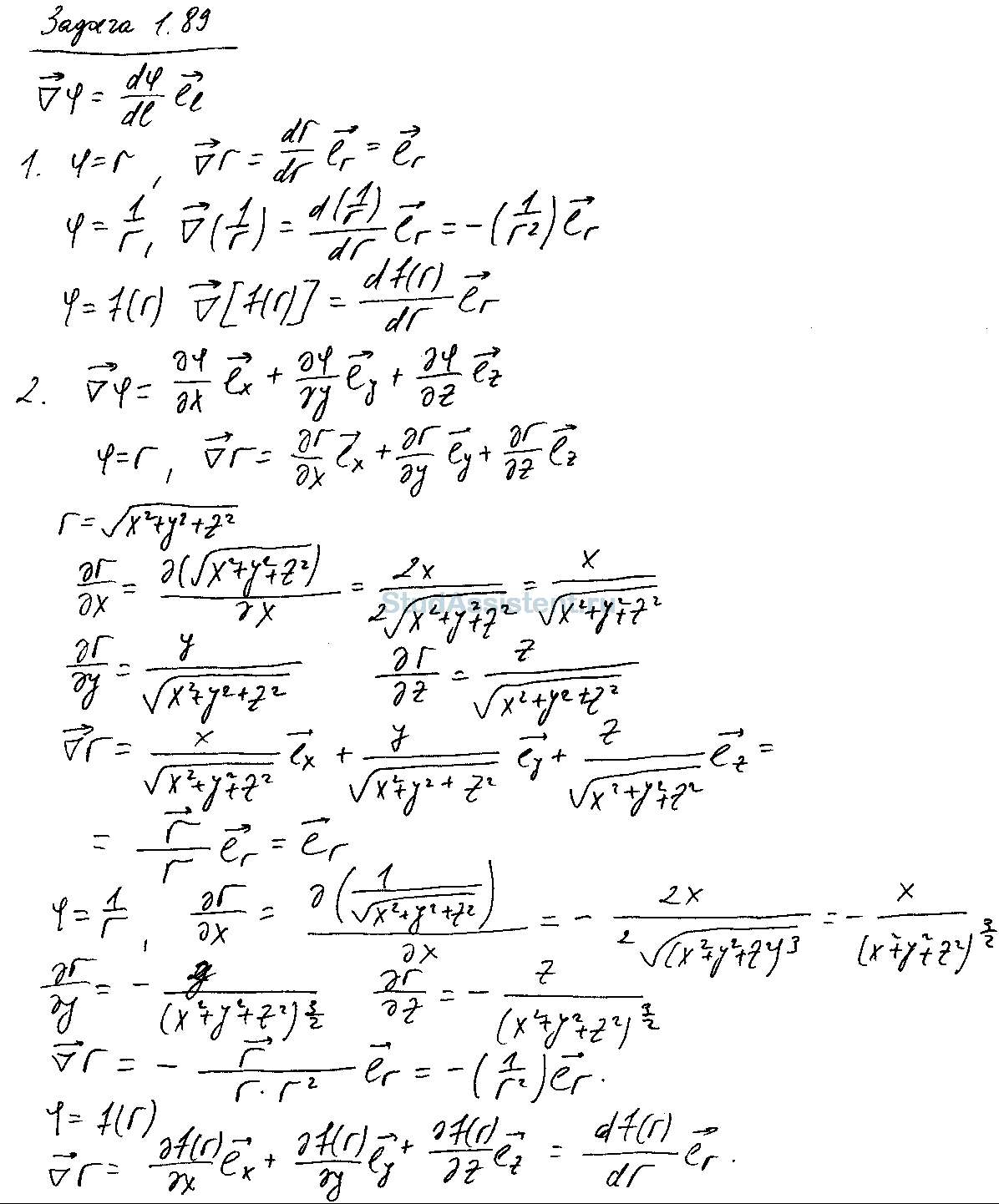Условие задачи 1.89:
Градиент скалярной функции φ в некоторой точке P представляет собой вектор, направление которого совпадает с направлением l, вдоль которого функция φ, возрастая по величине, изменяется в точке P с наибольшей скоростью. Модуль этого вектора равен значению dφ/dl в точке P. Аналитически это можно записать следующим образом:∇φ = (dφ/dl)el.
1. Исходя из этого определения, найти выражения для: а) ∇r, б) ∇(1/r), в) ∇f(r), где r — модуль радиус-вектора точки P.
2. Убедиться в том, что такие же выражения получаются с помощью формулы
∇φ = (∂φ/∂x)ex + (∂φ/∂y)ey + (∂φ/∂z)ez.